⌚시간 복잡도
- 시간 복잡도는 <문제를 해결하는데 걸린 시간과 입력의 함수 관계>를 의미한다. 보통 빅오 표기법으로 나타낼 수 있다. 시간복잡도는 효율적인 코드로 개선하는데 쓰이는 척도이다. 시간 복잡도가 낮을수록, 효율적인 알고리즘으로, 같은 작업을 하는 코드여도 구현에 따라 성능의 차이가 크게 발생한다.
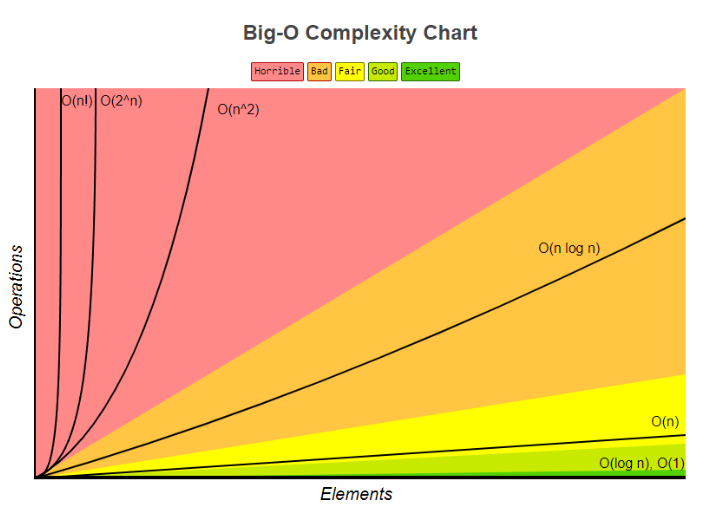
- Big O 표기법: 알고리즘 수행시간은 최악의 경우의 입력에 대한 기본 연산 횟수 수행시간이다.
- Big-O 표기 방식 (1)최고 차항만 남긴다. (2)최고 차항 계수(상수)는 생략한다. (3)Big-O(최고차항)로 표기한다. - Big-O (상한접근) : O(n) 최악의 경우 n번까지 수행되면 프로그램을 끝낼 수 있다. f(x)와 g(x) 두 함수가 있을 때 g(x)에 상수 c를 곱한 것이 f(x)보다 큰 경우가 존재하는 지를 확인하는 것.
Ex1) 2n + 10 is O(n) → 2n + 10 ≤ cn →(c-2)n ≥ 10 → n ≥ 10/(c-2) →Pick c = 3 and n0= 10
Ex2) n² is not O(n) →n² ≤ cn →n ≤ c → The above inequality cannot be satisfied since c must be a constant. - Big-Omega (하한접근) : 최적의 경우를 n번은 수행되어야 프로그램을 끝낼 수 있다.
- Big-Theta (평균접근) : Big-O와 Big-Omega의 평균
- 시간복잡도 표기 Constatnt time
- O(1) 상수 시간: 입력 크기에 상관없이 일정 연산을 수행하는 경우
int a = 10
- O(logN) 로그시간 Logarithmic time
for(i=1;i<n;i*2){ ... }
- O(n) 선형 시간 Linear time
for(i=0; i < n; i++) { ... }
- O(n²) 2차시간 Quadratic time
for(i=0; i < n; i++) {
for(j=0, j < n; j++) {
...
}
}
- O(2^n) 지수시간 Exponential time
int func (int n) {
if (n <= 1)
return n;
return func(n-1) + fun(n-2);
}
🧭공간 복잡도
- 공간 복잡도는 <프로그램을 실행시켰을 때 필요로 하는 자원 공간의 양>을 말한다. 정적 변수로 선언된 것 외에도 동적으로 재귀함수로 인해 공간을 계속해서 필요로 할 경우도 포함된다.
'CS > 자료구조' 카테고리의 다른 글
| [DS]Unit 2. Arrays and Lists(1) (0) | 2022.02.25 |
|---|---|
| [DS]Unit 1. Introduction(2) (0) | 2022.02.23 |
| [DS]Unit 1. Introduction(1) (0) | 2022.02.11 |